Love Letters

A belated post. During Valentine's Day, I entered several scripts into Wolfram's Sweet Tweet contest. Since Twitter is limited to 155 characters, the first was a shorter parametrization of the heart surface I described in an earlier post. Since it included the relation \(z^2+u^2=\left(\frac{1}{2}\right)^2\), it made more sense to replace \(z\) and \(u\) with \(\frac{1}{2}\cos t\) and \(\frac{1}{2}\sin t\), as they were just rectangular coordinates on a circle of radius \(\frac{1}{2}\). This gave a parametrization similar to that of a sphere with a variable radius.

The same insight inspired me to change my parametrization to the equivalent level surface \(x^2+4y^2+\left(z-\frac{1}{2}|x|\right)^2=1\), which used far fewer characters. The next script I uploaded was an Archimedean spiral of hearts, which has lots of potential interpretations. For some reason, it was popular.

Finally, I wanted to write the word "love" in cursive using a parametrized curve, so I used some graph paper to figure out the locations of the proper relative maximum and relative minimum values for the \(x\) and \(y\) coordinate functions, as functions of distance along the curve. Unfortunately, this ended with a degree 63 polynomial, which was both ridiculous and too long to fit into Twitter's 155 characters.

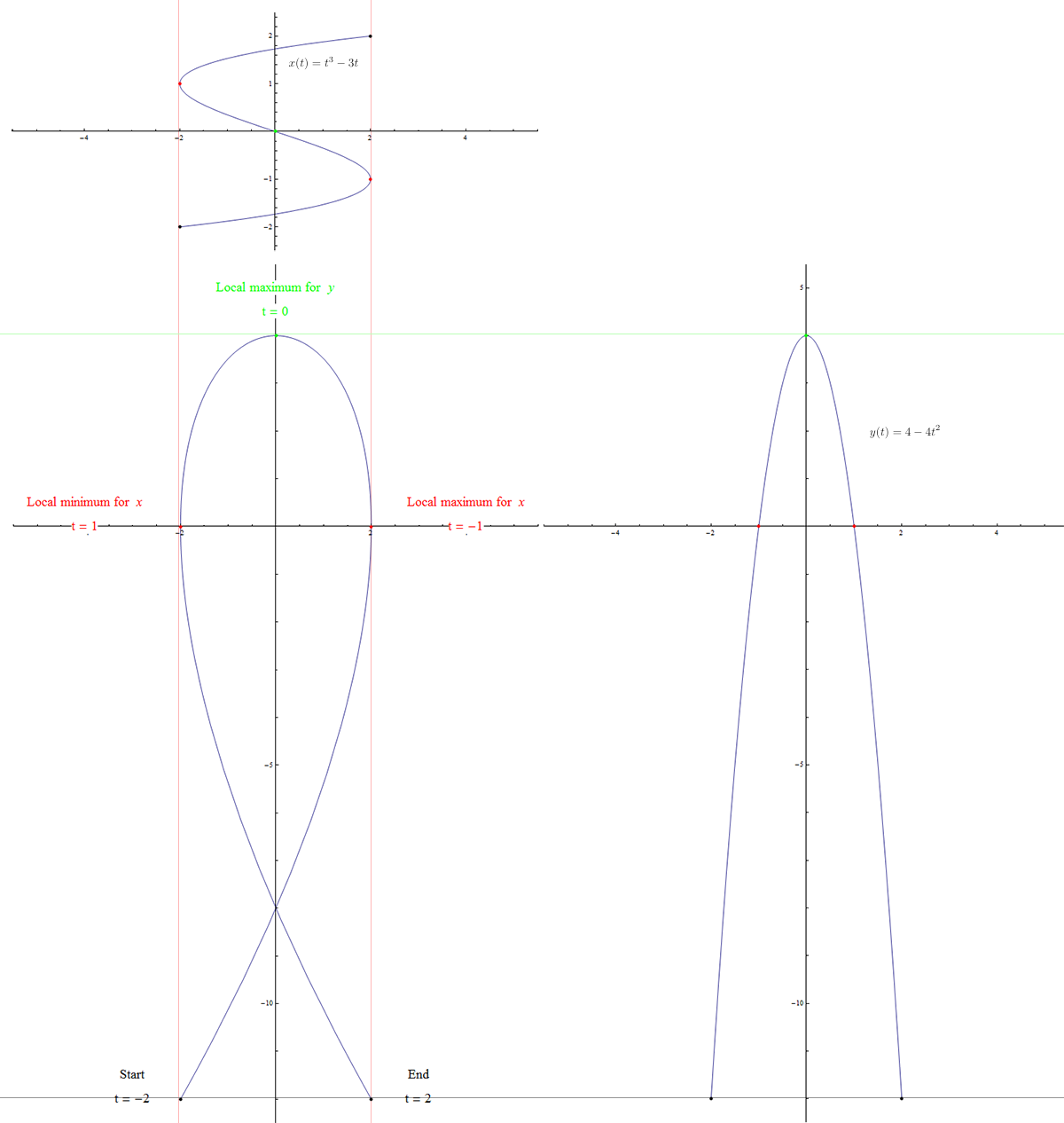
So I decided to write each letter individually. The cursive lowercase "l" shape was relatively simple: \(x(t)\) should have one local maximum and one local minimum, while \(y(t)\) should have one local maximum precisely halfway between the input values for the maximum and minimum of \(x(t)\).

Therefore, the simplest idea was to have \(x(t)\) be a cubic polynomial and \(y(t)\) be a quadratic polynomial. Suppose we want the local maximum value of \(x(t)\) to occur at \(t = 1\) and the local minimum value to occur when \(t = -1\). For a polynomial function, this means we want \(x'(t) = P(t + 1)(t - 1)\), which would guarantee those as critical points. The number \(P\) simply needs to be positive in order for the polynomial to be an increasing function for appropriately large magnitude values of \(x\), forcing the first critical point to be a local maximum and the second a local minimum. Choosing \(P = 1\), we have \(x'(t)=t^2-1\), which we can integrate to get \(x(t)=\frac{1}{3}t^3-t+C\). Setting \(C = 0\) makes the curve pass through \(x(0) = 0\), the halfway point between -1 and 1, so this cursive "l" will be symmetric about the \(y\) axis. Just to scale it up a little, and save some characters, we can multiply the polynomial by 3 to get \(x(t)=t^3-3t\).

Now for \(y(t)\), we want \(y(0)\) to be the maximum, and \(y\) must be quadratic in \(t\). So we want an inverted parabola like \(y(t)=-t^2\), and we want to lift it up a little so that the y values are positive for some interval between \(t = -1\) and \(t = 1\). I eventually decided on \(y(t)=-4t^2+4\) to get an aesthetically pleasing height to width ratio for the letter.

Putting these two coordinate functions together gives us the proper curve:

The "o" character was replaced with the heart shape from my previous post, and the "v" character was rendered using the absolute value function, truncated by a Boolean function so that it was not defined outside of a small interval. The same effect could have been accomplished algebraically, but would have once again used too many characters. (Exercise: Find an algebraic function whose graph is in the shape of the letter “v”, and which is naturally undefined outside of the interval which resembles the letter “v”, so that we don’t have to artificially restrict the domain ourselves.)

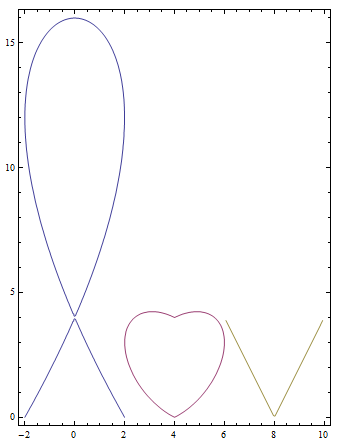
The interesting character of cursive "e" was accomplished by the same strategy used for laying out the cursive "l". First, we see there is one local maximum and one local minimum for \(x(t)\), and this time two local minimums and one local maximum for \(y(t)\), which makes it at least a quartic polynomial. The mathematics was done the same way, first specifying \(x'(t)\) as a product of root factors, then integrating the result. Then making sure the roots of \(y'(t)\) lay interspersed between the roots of \(x'(t)\) so that the result would be roughly an "e" shape. It is a fun exercise if you have the time.

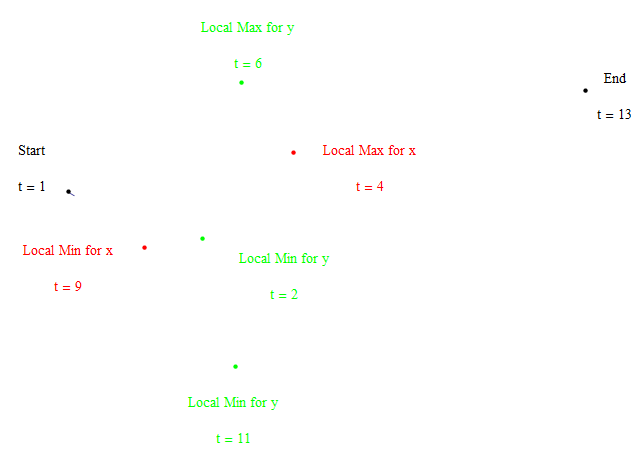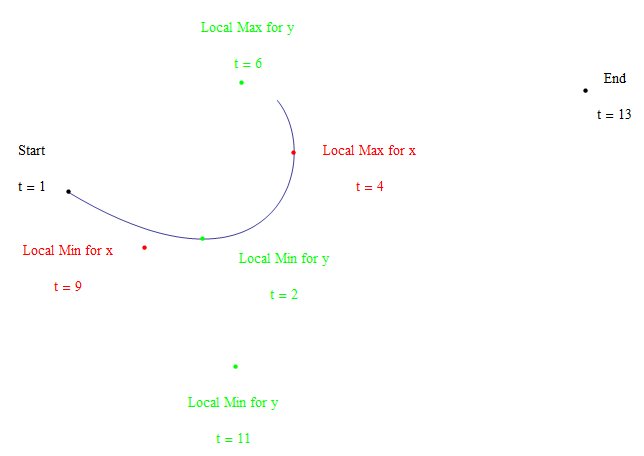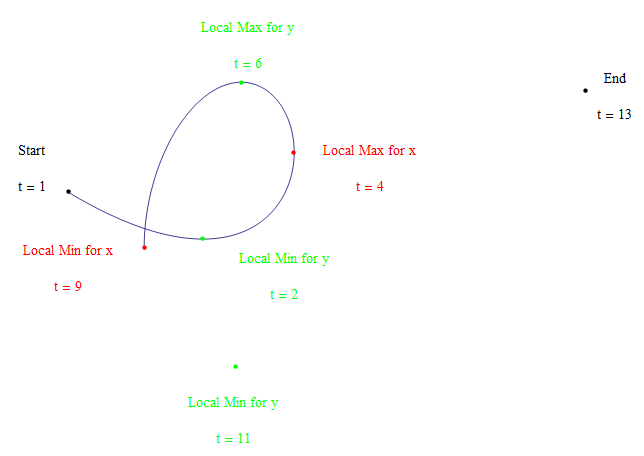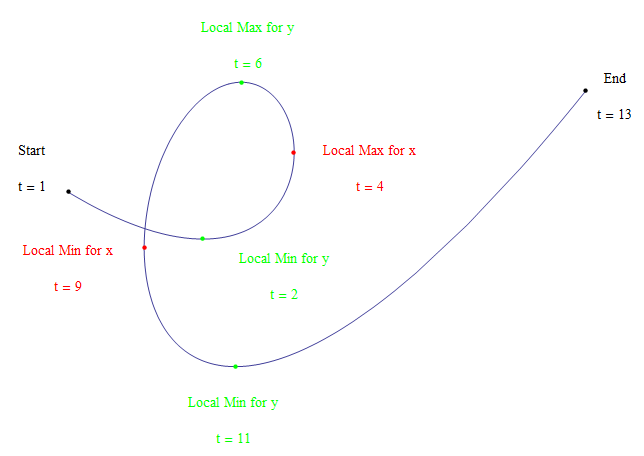
I chose to use \(x'(t) = k(t – 4)(t – 9)\) and \(y'(t) = p(t – 2)(t – 6)(t – 11)\), based on measuring arclengths on my own cursive “e” with string. The resulting integrated polynomials then needed to be multiplied by scaling factors so that the minimum and maximum values fell within the required range.

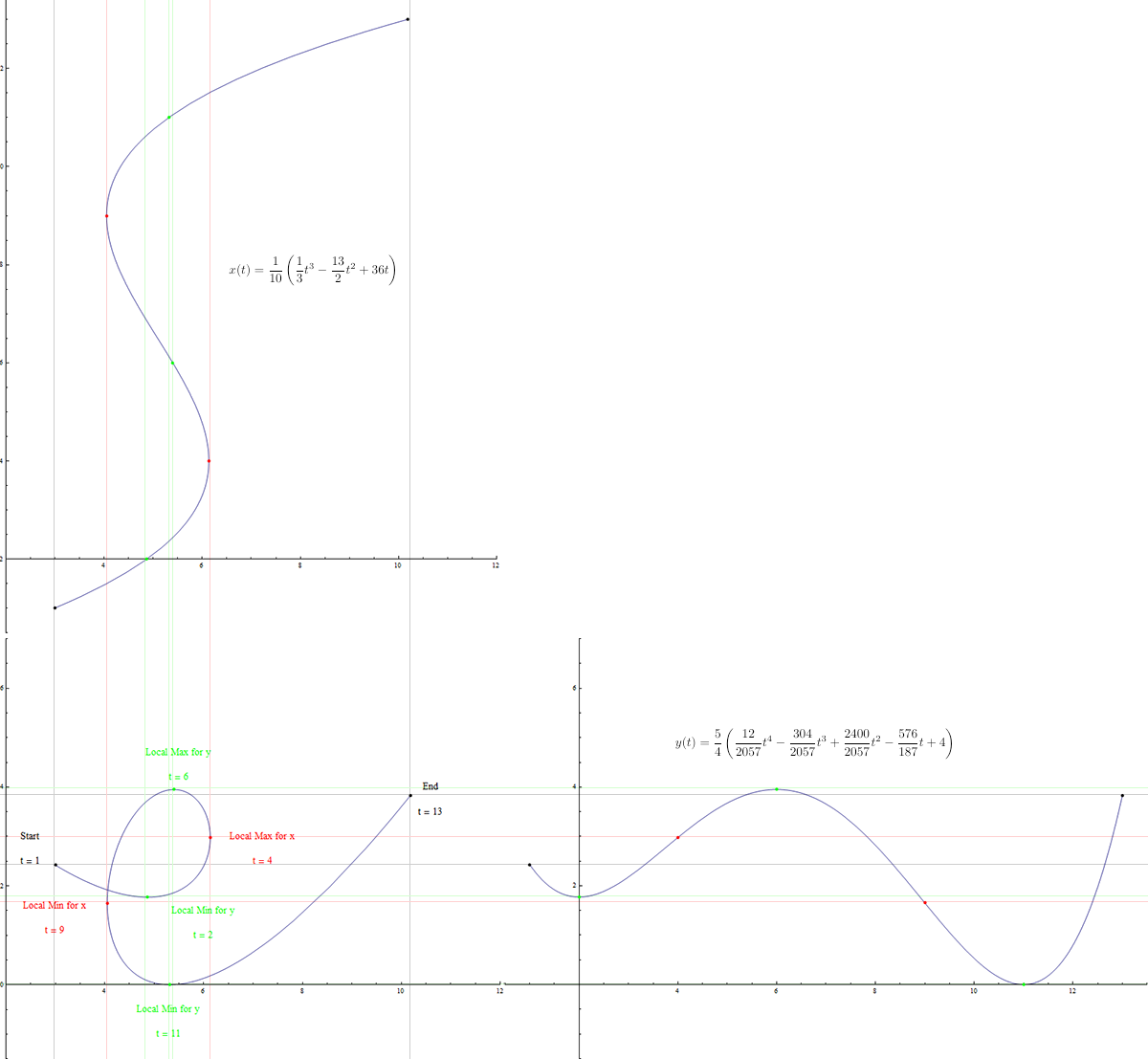
Unfortunately, even when using approximate decimal values for the fractions, this turned out to be a few too many characters for the Twitter challenge, so I ended up replacing the cursive "l" with a Tschirnhausen cubic and the cursive "e" with a folium of Descartes, but it was fun trying to make letters from polynomials. It may be fun to consider the rest of the alphabet as well.

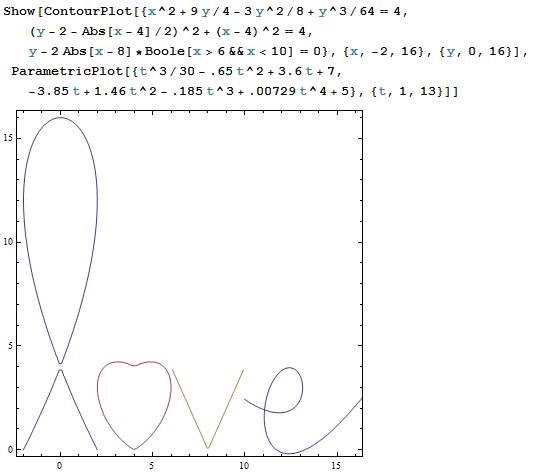
Of course, smooth cursive script may be more easily reproduced on computer screens using the Bézier method of constructing curves from tangent vectors attached to each point, but these resulting curves are usually made up of many polynomials, and, interestingly enough, even specifying the requisite list of points and the tangents for each point uses up more characters than the simpler polynomials above! At least I got a t-shirt out of it.